The Devious Sinc-Hole

The Borwein integrals are a mathematical oddity that manages to surprise even seasoned readers and hoarders of mathematical apocrypha. The unusual properties of the Borwein integrals were first presented in 2001 by the father-son duo of David and Jonathan Borwein and are a perfect example of the need for proof and rigor in math and the hazards of jumping to conclusions based on patterns that apparently hold for long sequences of numbers. The Borwein integrals are defined in terms of the sinc function

$\displaystyle \mathrm{sinc}(x) = \frac{\sin x}{x}, \; x \neq 0$

with $\mathrm{sinc}(0)=1$ . The Borweins described an astounding fact regarding integrals of products of sinc functions with suitably scaled arguments. Consider, for example, the pattern

$\displaystyle \int_{0}^{\infty} \mathrm{sinc}(x) \: \mathrm{d}x =\frac{\pi}{2},$

$\displaystyle \int_{0}^{\infty} \mathrm{sinc}(x) \cdot \mathrm{sinc}(x/3) \: \mathrm{d}x =\frac{\pi}{2},$

$\displaystyle \int_{0}^{\infty} \mathrm{sinc}(x) \cdot \mathrm{sinc}(x/3) \cdot \mathrm{sinc}(x/5) \: \mathrm{d}x =\frac{\pi}{2},$

and so on. Indeed, this pattern continues until the integral

$\displaystyle \int_{0}^{\infty} \mathrm{sinc}(x) \cdot \mathrm{sinc}(x/3) \cdot \ldots \cdot \mathrm{sinc}(x/13) \: \mathrm{d}x =\frac{\pi}{2}.$

Such a pattern would, without a doubt, tempt us to conclude that a similar result holds even with $\mathrm{sinc}(x/15)$ in the integrand. However, we have that

$\begin{aligned} \int_{0}^{\infty} \mathrm{sinc}(x) \cdot \mathrm{sinc}(x/3) \cdot \ldots \cdot \mathrm{sinc}(x/15) \: \mathrm{d}x &=\frac{467807924713440738696537864469}{935615849440640907310521750000} \pi \\ &=\frac{\pi}{2}-\frac{6879714958723010531}{935615849440640907310521750000} \pi \\ &\approx \frac{\pi}{2} - 2.31 \times 10^{-11}. \end{aligned}$

The Borweins, in their original paper [1] write, “When this fact was recently verified by a researcher using a computer algebra package, he concluded that there must be a “bug” in the software. Not so … This is a somewhat cautionary example for too enthusiastically inferring patterns from symbolic or numerical computation.”

So what is actually going on under the hood? Why does this pattern break down eventually? An intricate argument due to [2] using Fourier transform theory and convolutions explains why adding the $\mathrm{sinc}(x/15)$ term causes the general pattern to fail. To explain this, I will be assuming that the reader has some non-elementary familiarity of Fourier transforms and convolution. We first recall two facts:

The sinc function and the rectangular (boxcar) function are (provided they are suitably scaled) Fourier transform pairs of each other. This corresponds to the fact that the sinc filter is the ideal (brick-wall, or rectangular frequency response) low-pass filter.
Under some mild technical assumptions, convolution in the time domain amounts to multiplication in the Fourier (frequency) domain, and vice versa (provided that we properly scale the operations).

Since a convolution is the integral of a product, and what we’re looking to evaluate are integrals of products, we look at the multiplication in the frequency domain of the corresponding rectangular functions (that are the Fourier transforms of the sinc functions) and then consider the inverse Fourier transform of the aforementioned product. Consider the first term, i.e., $\mathrm{sinc}(x)$ which has a Fourier transform that is a rectangular pulse with a height of 1/2 and a half-width of 1 (there is a scaling factor of $1/ \pi$ that is suppressed in this discussion and I will defer the hands-on exercise of finding the actual values of the integrals to the end of the post, for now, we are motivated simply by why the pattern breaks down after a certain instant). We then keep convolving this rectangular pulse with similar pulses having half-widths 1/3, 1/5, 1/7, etc. The process is illustrated below (animation courtesy of Greg Egan https://twitter.com/gregeganSF/status/1041231747092897792):

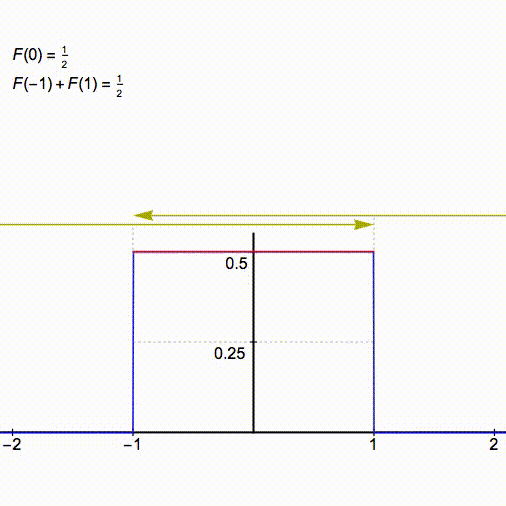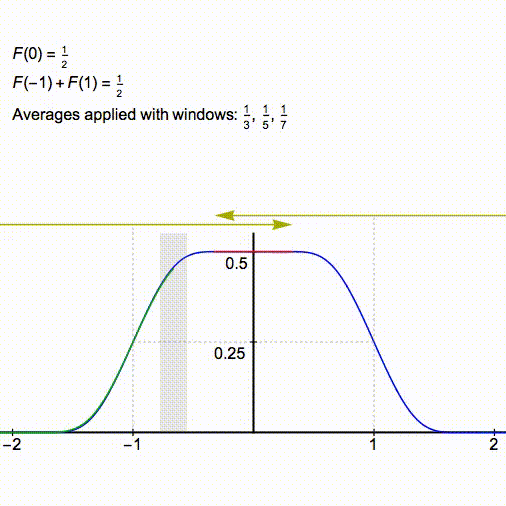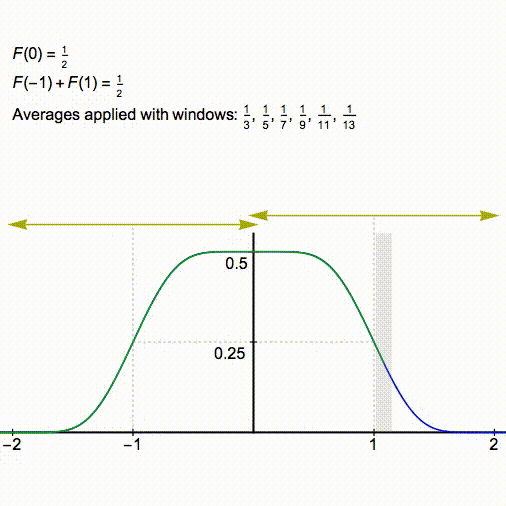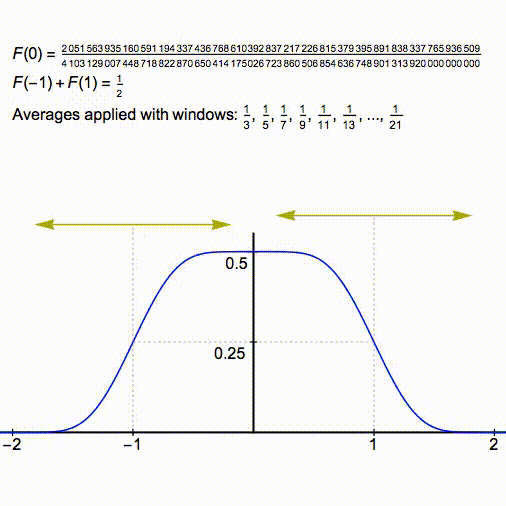
As the multiplications in the frequency domain keep on piling up on top of each other, something keeps changing! Initially, we have that the rectangular pulse of height 1/2 and half-width 1 passes through the point $(0,1/2)$ and the horizontal segment of top of the ‘plateau’ (marked in red in the above animation) has a width of exactly 2. However, the first convolution with half-width $1/3$ sloughs off a little bit from the flat top and the resulting curve has a half-width of $1 - 1/3$ . The second convolution with half-width $1/5$ sloughs off a little more and we’re left with a half-width of $1 - 1/3 - 1/5$ . Up until the point that $1 - 1/3 - 1/5 - 1/7 - \ldots$ remains positive, we have that the resultant curve passes through $(0,1/2)$ . The moment we have that $1 - 1/3 - 1/5 - 1/7 - \ldots < 0$ is when the top of the plateau gets completely eroded and the symmetry breaks down. It is then easy to see that

$\frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{9} + \frac{1}{11} + \frac{1}{13} = \frac{43024}{45045} < 1,$

but

$\frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{9} + \frac{1}{11} + \frac{1}{13} + \frac{1}{15} = \frac{46027}{45045} > 1.$

It is for this reason that adding the $\mathrm{sinc}(x/15)$ term causes the symmetry to break down and the remaining integrals in the pattern fail to have a value of $\pi/2$ .

Only one final part of the jigsaw remains to be placed. Why are the integrals equal to $\pi/2$ ? The integrands are all even functions and we have already seen that until we reach the break-even point where $\displaystyle \sum_{j=1}^7 \frac{1}{2j+1} > 1$ , all the multiplications by the rectangular pulses do not change the fact that the resultant pulse passes through the point $(0,1/2)$ and the resultant multiplications preserve the flat top of the plateau, and so it suffices to calculate

$\displaystyle I = \frac{1}{2} \int_{-\infty}^{\infty} \mathrm{sinc}(x) \: \mathrm{d}x.$

The (two-sided) Fourier transform of the sinc function is

$\displaystyle \mathcal{F} \{ \mathrm{sinc}(x) \}(\omega) = \int_{-\infty}^{\infty} \mathrm{sinc}(x) e^{-i \omega x} \: \mathrm{d}x = \pi \cdot \mathrm{rect} \left( \frac{\omega}{2} \right),$

which is a rectangular pulse with width 2 and height $\pi$ . Therefore,

$\displaystyle I = \frac{1}{2} \mathcal{F} \{ \mathrm{sinc}(x) \} (0) = \frac{\pi}{2},$

and we’re done!

These aren’t the only Borwein integrals. With suitable modifications, we can show that

$\displaystyle \int_0^{\infty} 2 \cos (x) \cdot \mathrm{sinc}(x) \cdot \mathrm{sinc}(x/3) \cdot \ldots \cdot \mathrm{sinc}(x/111) \: \mathrm{d}x = \frac{\pi}{2}$

but

$\displaystyle \begin{aligned} &\int_0^{\infty} 2 \cos (x) \cdot \mathrm{sinc}(x) \cdot \mathrm{sinc}(x/3) \cdot \ldots \cdot \mathrm{sinc}(x/111) \cdot \mathrm{sinc}(x/113) \: \mathrm{d}x \\ &< \frac{\pi}{2} \end{aligned}.$

A general intuition as to why this is true (not the complete explanation, though) can be obtained by noting that $2 \cos (x) \ \mathrm{sinc}(x) = \mathrm{sinc} (2x)$ and now, since the initial argument of the sinc function is scaled by a factor of 2, we have that

$\displaystyle \frac{1}{3} + \frac{1}{5} + \ldots + \frac{1}{111} <2,$

but

$\displaystyle \frac{1}{3} + \frac{1}{5} + \ldots + \frac{1}{111} + \frac{1}{113} > 2.$

Some very interesting recent work [3] (see [4] for a more digestible version) has also looked at an elegant reformulation of the above integrals from the point-of-view of random walks with a causality argument explaining the above phenomena and also opening the floodgates for a number of generalizations. That will be a story for some other day!

References:

[1] Borwein, D. and Borwein, J.M., 2001. Some remarkable properties of sinc and related integrals. The Ramanujan Journal, 5(1), pp. 73-89.

[2] Schmid, H., 2014. Two curious integrals and a graphic proof. Elemente der Mathematik, 69(1), pp. 11-17.

[3] Majumdar, S.N. and Trizac, E., 2019. When random walkers help solving intriguing integrals. Physical Review Letters, 123(2), Art. no. 020201.

[4] Hill, H.M., 2019. Random walkers illuminate a math problem. Physics Today, 72(9), pp. 18-19.

Share this:

Related

Leave a comment Cancel reply